Chapter 6 Accuracy, precision, and units
The science of measurements is called ‘metrology’, which, among other topics, focuses on measurement accuracy, precision, and units (Rabinovich, 2013). We will not consider these topics in depth, but they are important for statistical techniques because measurement, in the broadest sense of the word, is the foundation of data collection. When collecting data, we want measurements to be accurate, precise, and clearly defined.
6.1 Accuracy
When we collect data, we are trying to obtain information about the world. We might, for example, want to know the number of seedlings in an area of forest, the temperature of the soil at some location, or the mass of a particular animal in the field. To get this information, we need to make measurements. Some measurements can be collected by simple observation (e.g., counting seedlings), while others will require measuring devices such as a thermometer (for measuring temperature) or scale (for measuring mass). All of these measurements are subject to error. The true value of whatever it is that we are trying to measure (called the ‘measurand’) can differ from what we record when collecting data. This is true even for simple observations (e.g., we might miscount seedlings), so it is important to recognise that the data we collect come with some uncertainty. The accuracy of a measurement is defined by how close the measurement is to the true value of what we are trying to measure (Rabinovich, 2013).
6.2 Precision
The precision of a measurement is how consistent it will be if measurement is replicated multiple times. In other words, precision describes how similar measurements are expected to be (Wardlaw, 1985). If, for example, a scale measures an object to have the exact same mass every time it is weighed (regardless of whether the mass is accurate), then the measurement is highly precise. If, however, the scale measures a different mass each time the object is weighed (for this hypothetical, assume that the true mass of the object does not change), then the measurement is not as precise.
One way to visualise the difference between accuracy and precision is to imagine a set of targets, with the centre of the target representing the true value of what we are trying to measure (Figure 6.1)3.
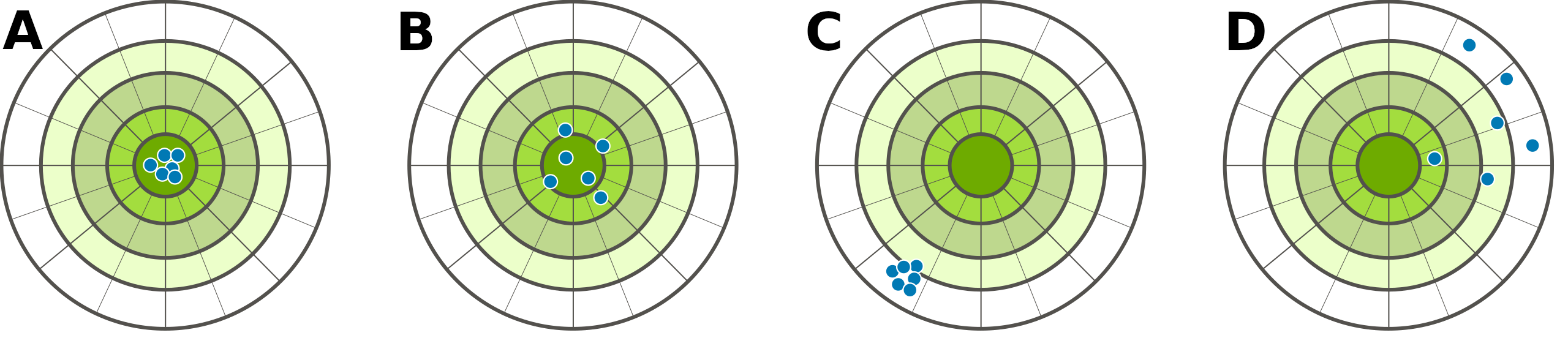
Figure 6.1: Conceptual figure illustrating the difference between accuracy and precision. Points in A are both accurate and precise, points in B are accurate but not precise, points in C are precise but not accurate, and points in D are neither accurate nor precise.
Note again that accuracy and precision are not necessarily the same (Dytham, 2011). Measurement can be accurate but not precise (Figure 6.1B) or precise but not accurate (Figure 6.1C).
6.3 Systems of units
Scientific units are standardised with the Système International D’Unités (SI). Having standardised units of measurement is highly important to ensure measurement accuracy (Quinn, 1995). Originally, these units were often defined in terms of physical artefacts. For example, the kilogram (kg) was once defined by a physical cylinder of metal housed in the Bureau International des Poids et Mesures (BIPM). In other words, the mass of a metal sitting at the BIPM defined what a kilogram was, with the mass of every other measurement being based on this physical object (Freedman et al., 2011; Quinn, 1995). This can potentially present a problem if the mass of that one object changes over time, thereby causing a change in how a kilogram is defined. Where possible, it is therefore preferable to define units in terms of fundamental constants of nature. In 2019, for example, the kilogram was redefined in terms of the Planck constant, a specific atomic transition frequency, and the speed of light (Stock et al., 2019). This ensures that measurements of mass remain accurate over time because what a kilogram represents in terms of mass cannot change.
We can separate units into base units and derived units. Table 6.1 below lists some common base units for convenience (Quinn, 1995). You do not need to memorise these units, but it is good to be familiar with them. We will use these units throughout the book.
| Measured Quantity | Name of SI Unit | Symbol |
|---|---|---|
| Mass | kilogram | kg |
| Length | metre | m |
| Time | second | s |
| Electric current | ampere | A |
| Temperature | kelvin | K |
| Amount of a substance | mole | mol |
| Luminous intensity | candela | cd |
We can also define derived SI units from the base units of Table 6.1 (Gupta, 2020). Examples of these derived SI units are provided in Table 6.2. Again, you do not need to memorise these units, but it is good to be aware of them.
| Measured Quantity | Name of Unit | Symbol | Definition in SI Units |
|---|---|---|---|
| Area | square metre | \(A\) | m2 |
| Volume | cubic metre | \(V\) | m3 |
| Speed | metre per second | \(v\) | m s-1 |
| Mass density | kilogram per metre | \(\rho\) | kg m-3 |
| \(\hspace{2mm}\)cube | |||
| Amount | mole per cubic | \(c\) | mol m-3 |
| \(\hspace{2mm}\)concentration | \(\hspace{2mm}\)metre | ||
| Force | newton | \(N\) | m kg s-2 |
| Pressure | pascal | \(Pa\) | m-1 kg s-2 |
| Energy | joule | \(J\) | m2 kg s-2 |
When numbers are associated with units, it is important to recognise that the units must be carried through and combined when calculating an equation. As a very simple example, if we want to know the speed at which an object is moving, and we find that it has moved 10 metres in 20 seconds, then we calculate the speed and report the correct units as below,
\[speed = \frac{10\:\mathrm{m}}{20\:\mathrm{s}} = 0.5\:\mathrm{m}/\mathrm{s} = 0.5\:\mathrm{m}\:\mathrm{s^{-1}}.\]
Notice that the final units are in metres per second, which can be written as m/s or m s-1 (remember that raising s to the \(-1\) power is the same as 1/s; see Chapter 1 for a reminder about superscripts). Recognising that units are also part of calculations is important.
References
This figure was released into the public domain by Egon Willighagen on 8 March 2014: https://commons.wikimedia.org/wiki/File:Accuracy-vs-precision-nl.svg↩︎